\(^▽^)/
アロハ~!
しあわせ探検家の晋作です!
ご機嫌いかがですか?
さて、「CAMRの胎動-解題!実用理論辞典」シリーズの続きで、今回は位相空間です。
まずは、論文を見てみましょう。
★☆★☆★☆★☆★☆★☆以下引用★☆★☆★☆★☆★☆★☆
「位相空間の中では、ある一瞬の力学系についての全情報は一点に集まる」のである。もしこれが本当なら素晴らしいことではないだろうか。先に「アフォーダンス(その2)」のところで述べたように、運動を構成する様々な要素とその相互作用に関するすべての情報を含んだ結果を、一つの点としてこの図では見ることができるかもしれない。
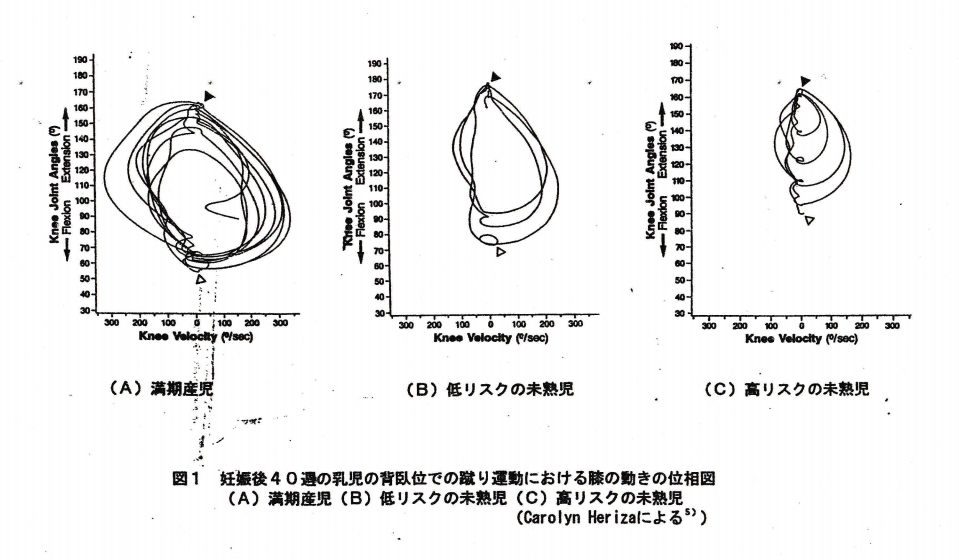
図1を見ていただきたい。これは満期産乳児(A)、低リスクの未熟児(B)、高リスクの未熟児(C)の妊娠後40週における、背臥位での蹴り運動時の一側の膝の動きを表したものだ。膝の速度と位置が一点で表されている。速度と位置という二つの軸からなる二次元の平面が、この場合の位相空間となる。乳児の運動は一瞬一瞬に変化するから、時間の経過とともに位相空間の中の点も移動する。それぞれの図の軌跡は、3分間に起きた運動の変化をたどったものだ。
満期産児の図は、大まかに8つの円を描いている。つまり3分間に8回の周期運動を繰り返している。一番動きが速く、運動の範囲も大きい。その軌跡は空間内のある範囲に留まっていることが分かる。低リスク児の軌跡は、3回の周期運動しか見せていない。運動の速度が低く、運動範囲も小さい。しかしながらこの軌跡も満期産児のものと同様に閉じた円を描いている。つまりパターン自体あるいは運動の質は満期産児と変わらないことが視覚的に理解できる。
このように運動がある領域内に留まっている場合、その領域をアトラクター領域と呼ぶ。この場合、アトラクター領域は閉じた円を描いているので周期的なアトラクターと呼ばれる。これは十分納得のいくことで、蹴る、走る、ジャンプなどの下肢運動は普通、周期運動である。このようなアトラクターは、膝の角度や速度に一定した関係があること、すなわち私たちがよく言うところの協調性があることを示している。
高リスク児は、運動範囲も小さく速度も低い。しかも満期産児等に比べてアトラクター領域はより広い範囲に分散する。高リスク児の運動は角度や速度に安定した関係が築かれていない。このように位相空間を使うことによって、運動の特徴を理解しやすくなるのである。
ただし、この場合の位相空間上の一点はそのシステムに関わる全ての情報を含んでいるわけではない。それでもⅡSTEP会議のセラピスト達は、以下のように説明している。「人の運動システムは高次元なシステムだが、低次元に振る舞う。」つまり人の運動を構成する要素はたくさんあるから、情報を与える点が存在する空間は、速度と位置だけを持った二次元平面ではなく、もっとたくさんの軸を持った多次元空間が必要かといえばそうでもない。それは結局低次元に振る舞うのだから二次元平面で充分だということらしい。
★☆★☆★☆★☆★☆★☆引用終わり★☆★☆★☆★☆★☆★☆
位相空間というものは、「現代科学の最も強力な発明の一つ」とも言われているそうです。
こう書くといろんな声が聞こえてきそうです。
「うん、その通りだ!」、「そんな大袈裟な!」、等々。
さて、あなたの反応はどちらでしょうか?
僕は前者でした。なぜなら、物理空間の呪縛から解放されるからです。僕たちはどうしても視覚情報の影響を大きく受けるので、目に見える物理空間というのはとてもわかりやすく、絶大な信頼を置いています。あたかも、物理空間こそが宇宙を支配する王様であるかのように。
それなのに、この位相空間というやつは、なんてことをしでかしてくれるのでしょう。たった二つの要素を軸にするだけで、これまで目に見えなかった運動の特徴を、見事に描き出しているではないですか。
そう考えると、今、目に見えている世界を僕たちはどの程度理解しているのか怪しいものです。これまで絶大な信頼を寄せていた物理空間からでさえ、十分な情報を得られていなかったわけですので。
見えないものを見える化する。そんな力が位相空間にはあるんですね。
【引用・参考文献】
西尾幸敏:実用理論事典-道具としての理論(その1).上田法治療研究会会報, No.18, p17-29, 1995.
西尾幸敏:実用理論事典-道具としての理論(その2).上田法治療研究会会報, No.19, p1-15, 1995.
西尾幸敏:実用理論事典-道具としての理論(その3).上田法治療研究会会報, Vol.8 No.1, p12-31, 1996.
西尾幸敏:実用理論事典-道具としての理論(その4).上田法治療研究会会報, Vol.8 No.2, p76-94, 1996.
西尾幸敏:実用理論事典-道具としての理論(その5).上田法治療研究会会報, Vol.8 No.2, p120-135, 1996.
西尾幸敏:実用理論事典-道具としての理論(その6 最終回).上田法治療研究会会報, Vol.8 No.3, p120-135, 1996.
最後まで目を通していただき、ありがとうございます!
あなたにすべての良きことが雪崩のごとく起きます!
マハロ~!
p.s.ブログランキング参加中!ご協力ありがとうございます!!


\(^▽^)/
アロハ~!
しあわせ探検家の晋作です!
ご機嫌いかがですか?
さて、「CAMRの胎動-解題!実用理論辞典」の続きです。
今回は「アフォーダンス(その3)」です。
まずは、論文を見てみましょう。
★☆★☆★☆★☆★☆★☆以下引用★☆★☆★☆★☆★☆★☆
誤解してはいけないのは、アフォーダンスは観察者の要求や状況によって、対象物に与えられる性質ではない。物が本来持っている誰にでも与えられる公共性のある情報なのである。
たとえば、ある人にはむき身のカキは「気持ち悪いよ」と語りかけるかもしれない。だからといってカキの食べれるという物理的な性質が変わるわけではない。カキは誰に対しても多くの情報を提供する。しかし、その情報を見つけ取り上げるのは、受け手の能力や状態であったりする。
「だからどうした」という読者の声が聞こえそうだ。「まるっきりのたわごとではないか」と。まったくだ。今のところ、このアイデアは脳性運動障害を理解することをアフォードしそうにないではないか。少し具体例を出さなければ。
「還元主義(その1)※」のところで父親の例を出した。自転車と壁の間の隙間を通るところをもう一度考えてみよう。最初壁と自転車で作られた隙間を前に、父親は通り抜けれないと言い、横歩きの戦略が出た後では、「通れるかも知れない」と言っている。この変化をどう理解したらいいだろうか?
※「還元主義(その1)」の該当部位は以下の通りです。
////////////////////////////////////////////////////////
自転車と壁の間の細い通路を前にして、父親は「わしはここを通れん。自転車を倒すじゃろう。」と言った。私の返事は、「横向きに歩いたら?」だ。父親は少なくとも家に帰ってからは、横歩きの練習などしたことがない。父親は思案した上、健側・患側それぞれの方向への横歩きを試した。結局、「通れるかもしれんのう」と言い、健側方向への横歩きで通り抜けた。
////////////////////////////////////////////////////////
還元主義では、要素に分解していく。この場合は、認知という要素が変化したのかも知れない。さて認知はどのように変化したのか、どの程度変化したのか?認知の変化の程度はどの程度、「通れる」「通れない」という結果に反映されるだろうか?
これを明確にしようとするのが還元主義的アプローチであるにも関わらず、これを明確にできないのが現状である。また仮に明確にしたところで、状況が異なれば変化してしまう、ごく一時的で特殊な関係に過ぎないかもしれない。
水はどんなに見た目が変わろうともH2Oだが、認知と「通れる」「通れない」の間の関係など、あやふやでいくらでも変化しそうである。つまり他の場面で応用のできるような普遍的な関係ではない。ただし、少なくともこれまでの物の見方、枠組みでは難しいということだ。
★☆★☆★☆★☆★☆★☆引用終わり★☆★☆★☆★☆★☆★☆
アフォーダンスは公共性のある情報だということですが、これまでの物の見方、枠組みではアフォーダンスを理解することは難しい、とも述べられていますね。
何が難しいのかと言いますと、従来の物の見方とは異なるパラダイムを理解する必要があるからです。前回「ギブソンの主張はまるで、従来的な科学へ挑戦状を叩きつけているかのようですね」と書きましたが、それはまさしくギブソンが従来的な物とは異なるパラダイムを提唱しているからです。
この部分については、少し説明をしておかないと次へ進みにくいと思いますので、次回から一旦「アフォーダンス」を中断して取り上げていきます。
【引用・参考文献】
西尾幸敏:実用理論事典-道具としての理論(その1).上田法治療研究会会報, No.18, p17-29, 1995.
西尾幸敏:実用理論事典-道具としての理論(その2).上田法治療研究会会報, No.19, p1-15, 1995.
西尾幸敏:実用理論事典-道具としての理論(その3).上田法治療研究会会報, Vol.8 No.1, p12-31, 1996.
西尾幸敏:実用理論事典-道具としての理論(その4).上田法治療研究会会報, Vol.8 No.2, p76-94, 1996.
西尾幸敏:実用理論事典-道具としての理論(その5).上田法治療研究会会報, Vol.8 No.2, p120-135, 1996.
西尾幸敏:実用理論事典-道具としての理論(その6 最終回).上田法治療研究会会報, Vol.8 No.3, p120-135, 1996.
最後まで目を通していただき、ありがとうございます!
あなたにすべての良きことが雪崩のごとく起きます!
マハロ~!
p.s.ブログランキング参加中!ポチッと押していただけるととても励みになります!!


【CAMR情報】
CAMR基本テキスト、CAMR公式Facebookページ、CAMR公式ホームページ
【経済的自由人への道】
オンライン投資スクール、クリプトピースプロジェクト
\(^▽^)/
アロハ~!
しあわせ探検家の晋作です!
ご機嫌いかがですか?
さて、「CAMRの胎動-解題!実用理論辞典」の続きです。
前回「アフォーダンス」の導入の部分を紹介させていただきました。今回は、
その続きです。
まずは、論文を見てみましょう。
★☆★☆★☆★☆★☆★☆以下引用★☆★☆★☆★☆★☆★☆
アフォーダンスはギブソンの造語である。基になっているのはアフォードと言
う動詞で、「~できる、提供する」という意味を持つ。アフォーダンスとは環
境に存在する事物から、動物(人を含む)に与えられる価値や意味である。こ
れまでのところ、価値や意味は人が判断するものであると考えられている。と
ころがギブソンは、見る者によって左右されない普遍的な価値が物から提供さ
れると考えているのである。
たとえば、ある人がむき身のカキ(牡蛎)を見たとする。これまでの考えで
言うなら、過去に「食べることができる」という見るなり聞くなり食べるなり
の経験をしており、それを基にカキが自分に取って食物であるという意味を人
は判断するのである。しかしギブソンによるとそうではない。むき身のカキは
もともと「食べれるよ」と語りかけているのである。しかも観察者(つまり私
たちを含む動物)が空腹かどうかに関わりなく、語りかけているのである。
一つの物体はたくさんの情報を提供しており、どの情報が受け取られるかは
観察者との相互作用の結果による。台所の食卓の前の椅子を考えてみよう。普
通この椅子は「座って」と語りかける。このことを座ることをアフォードする
と表現しよう。幼児なら這いあがることをアフォードする。ゆで卵を持ったと
きに、座面でコンコン殻を割ることをアフォードするかも知れない。あるいは
夫婦喧嘩の中では、相手を打ち据えるために振り上げることをアフォードする
かも知れない(わが家の話ではない)。棚の上の物を取るときには、その上に
立つことを・・・きりがないのでやめる。
椅子が無限のアフォーダンスを持つように、私たちの暮らす環境も無限のア
フォーダンスを含んでいる。それらは知覚すべき物として常に存在する。それ
らにどのような価値を見いだすかは、観察者による。
★☆★☆★☆★☆★☆★☆引用終わり★☆★☆★☆★☆★☆★☆
ここで、「アフォーダンスとは何か?」という部分が語られています。従来的
な考え方では、ある現象の意味や価値は、人が見い出すものだと考えられてい
ました。
しかし、ギブソンは環境からも普遍的な情報が提供されていると言います。結果
として、両者の相互作用によって、その時その場の状況に応じて、情報の意味
や価値が決まることになります。
ギブソンの主張はまるで、従来的な科学へ挑戦状を叩きつけているかのようで
すね。なぜなら、従来的な科学では「再現性」というものが重視され、「その時その場の状況によって、、」などという曖昧さは、徹底的に排除したいことのはずだからです。
はてさて、この後の展開やいかに・・
【引用・参考文献】
西尾幸敏:実用理論事典-道具としての理論(その1).上田法治療研究会会報
, No.18, p17-29, 1995.
西尾幸敏:実用理論事典-道具としての理論(その2).上田法治療研究会会報
, No.19, p1-15, 1995.
西尾幸敏:実用理論事典-道具としての理論(その3).上田法治療研究会会報
, Vol.8 No.1, p12-31, 1996.
西尾幸敏:実用理論事典-道具としての理論(その4).上田法治療研究会会報
, Vol.8 No.2, p76-94, 1996.
西尾幸敏:実用理論事典-道具としての理論(その5).上田法治療研究会会報
, Vol.8 No.2, p120-135, 1996.
西尾幸敏:実用理論事典-道具としての理論(その6 最終回).上田法治療研
究会会報, Vol.8 No.3, p120-135, 1996.
最後まで目を通していただき、ありがとうございます!
あなたにすべての良きことが雪崩のごとく起きます!
マハロ~!
p.s.ブログランキング参加中!ポチッと押していただけるととても励みになり
ます!!


【CAMR情報】
CAMR基本テキスト、CAMR公式Facebookページ、CAMR公式ホームページ
【経済的自由人への道】
オンライン投資スクール、クリプトピースプロジェクト